Deductum
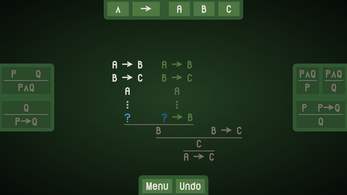
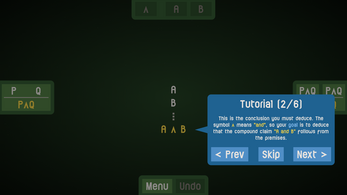
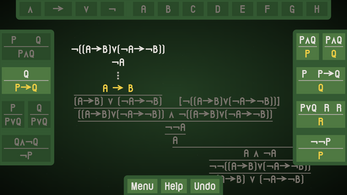
In this minimalistic puzzle game, you're given a set of premises and a conclusion, and your task is to use the fundamental rules of logic to formally prove, step by step, that the conclusion follows.
Tutorials introduce you to the world of proofs and the game mechanics. The early problems are simple, but the difficulty gradually increases until eventually you might not even know where to begin. Still, every problem has a solution, and if you think deeply enough, you'll never need to guess!
- Simple controls. No timers. No distractions. Just logic.
- 111 problems to solve, including classic theorems like De Morgan's Laws and the Law of the Excluded Middle
- Sandbox mode: enter any claim (with proposition symbols A–H) and see if you can prove it!
NOTE: To run the MacOS version, double clicking may not work. Instead, try right-clicking the app and choosing 'Open' in the menu and then again 'Open' in the confirmation dialog.
Purchase
In order to download this game you must purchase it at or above the minimum price of $5 USD. You will get access to the following files:
Development log
- Level names addedJan 11, 2026
- Version 1.0 released, with free demoMay 18, 2025
Comments
Log in with itch.io to leave a comment.
I just bought the full game (mac) and it said the file is damaged. Any solutions, nonpop?
How did you open it? Sometimes you can't just double click but have to right-click the app and choose "Open" in the menu, and then again "Open" in the confirmation dialog. I think this is only needed once and then it works normally. Unfortunately I don't have access to a Mac anymore so I can't verify.
I really enjoyed the demo! It took me a few rounds to get the hang of it, but once I did it was really fun!
Good to hear, thanks!
Is first order logic included in the later levels?
No, this is propositional logic only. I have plans for adding first order logic (likely as a separate game as it would probably need some bigger UI changes) too but haven't had time to do it yet
Loved the demo! Would really love to get a function to copypaste the deduction tree you already have, like if you proved in the left subbranch that the statement D is true, you could just drag over the same reasoning tree to the right branch if it is needed, like in the last level of the demo
Thanks! Yeah, such a function could be useful in some places but I think in *most* cases you can find a shorter sub-proof so that it's easy to copy manually ;) I'll keep it in mind for a possible future extension/v2 though!
I agree, but what would be more useful is instead of copy-pasting the same thing everywhere, you write it once and you can reuse it like a function. This will require it to be able to be extracted as a separate tree and then be referenced when needed.
Do you mean essentially like a custom "rule" (lemma) which you could then use like an ordinary rule wherever it fits? So basically a kind of template instead of a plain copy.
Fun game, very repetitive though. Kind of fun to switch you brain off and just play off vibes
Thanks for the comment! Glad you're having fun :)
I don't get it, but i like it
I'll count that as success :)
it would be so convenient if we could also go forward from the premises so we don't have to prove B is true 3 times
You're right, I even had it at some point but decided to remove it to simplify the UI since not many levels seemed to need it. But you're not the first one to comment about it so maybe I was wrong...
I love backwards solving the “crab” way, but it is also very useful to solve forward. Maybe you could dynamically hide the forward-solving elements of the UI if the level doesn’t need it, but also let the player take control over it just in case i want to do something you didn’t expect.
I'll keep this idea in mind 👍
The full version does not include:
<-> (implies and vise versa)
-/> (does not imply)
<-
</-
Extra proofs:
A, A -/> B | not B
A, A <-> B | B
not A, A <-> B | not B
Thanks for the comment! I indeed dropped equivalence (<->) because I thought it would clutter the UI without bringing interesting new mechanics. Maybe I'll include it in a future version, though. I'll also add your proof suggestions to a list of possible future additions!
More proofs: A <-> B | A -> B, B -> A
A -> B | A -/> not B
A -/> B | A -> not B
not not A | B
A -> B | B -> A
A <-> B | A -> B, B -> A
A and B | A <-> B
not A and not B | A <-> B
A <-> B | A and B or not A and not B
not A <-> B | not A and B or A and not B
Level ideas:
1.
Premise: A -/> B
Prove: A -> not B
2.
Premises: A -> B, B -/> C
Prove: A -> not C
3.
Premise: A -/> not B
Prove: A -> B
4.
Premise: A <-> B
Prove: A -> B and B -> A
5.
Premise: A and B
Prove: not(A -/> B)
6.
Prove: (not A) -/> A
7.
Prove: (A and A-/> B) -> (A <-> B)